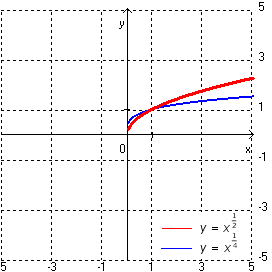
dla k=1,2,3,...
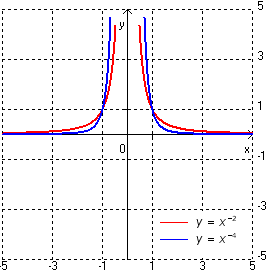
y=x4
...
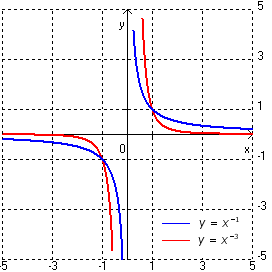
dla k=1,2,3,...
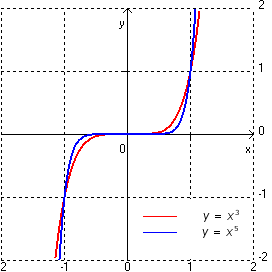
y=x3
...
- Dziedzina to zbiór R
- Miejsce zerowe: x=0
- Funkcja jest rosnąca w przedziale (0;+∞)
- Funkcja jest malejąca w przedziale (-∞0)
- Funkcja nie jest różnowartościowa
- Funkcja jest ciągła
- Dziedzina to zbiór R
- Miejsce zerowe: x=0
- Funkcja jest rosnąca
- Funkcja jest różnowartościowa
- Funkcja jest ciągła