Zdaniem w logice nazywamy takie wyrażenie, któremu jednoznacznie można przyporządkować jedną z dwóch wartości: prawdę lub fałsz. Prawdę oznaczamy symbolem 1, a fałsz 0.

       Zdania w logice oznaczamy literami: p, q, r, s, t itd.

   Zaprzeczenie zdania p oznaczamy symbolem ~ p i czytamy:,, nieprawda, że p...”

     Zdania proste p i q połączone spójnikiem  tworzą koniunkcję zdań. Koniunkcja zdań jest prawdziwa tylko wtedy, gdy oba zdania proste są prawdziwe.

      Zdania proste p i q połączone spójnikiem  tworzą alternatywę zdań. Alternatywa zdań jest fałszywa tylko wtedy, gdy oba zdania proste są fałszywe.

      Zdania proste p i q połączone spójnikiem  tworzą implikację zdań. Zdanie p nazywamy poprzednikiem implikacji a zdanie q –następnikiem. Implikacja zdań jest fałszywa tylko wtedy, gdy poprzednik jest prawdziwy a następnik fałszywy.

     Zdania proste p i q połączone spójnikiem  tworzą równoważność zdań. Zdanie pjest prawdziwe tylko wtedy, gdy oba zdania proste mają tę samą wartość logiczną.

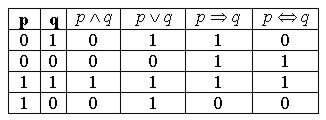
Przykłady:

p: Wisła wpada do Bałtyku                                               prawda(1)

~ p: Wisła nie wpada do Bałtyku                                      fałsz (0)

q:                                                                             prawda (1)

~q:                                                                           fałsz (0)

r: Delfin jest ssakiem                                                      prawda (1)

s: Delfin jest rybą                                                            fałsz (0)

Delfin jest ssakiem i rybą                                                fałsz (0)

Delfin jest ssakiem lub rybą                                             prawda (1)

      Delfin jest ssakiem tylko wtedy , gdy jest rybą             fałsz (0)

      Jeśli delfin jest ssakiem, to jest rybą                              fałsz (0)

    A oto kilka zdań, które są tautologiami:

a) ~ (         zaprzeczenie koniunkcji jest równoważne sumie zaprzeczeń

b) ~ (         zaprzeczenie alternatywy jest równoważne koniunkcji zaprzeczeń  

Zdania a) i b) nazywamy prawami de Morgana                  

c) ~ (

d) [p

e) [p

f) [(p

g)

h) [(

      Aby sprawdzić, czy dane zdanie jest tautologią stosujemy metodę zero- jedynkową. Najprościej jest taki dowód przeprowadzić w tabelce.

    

      Udowodnię, że zdanie e) jest tautologią (metodą ,,zero- jedynkową”):

 

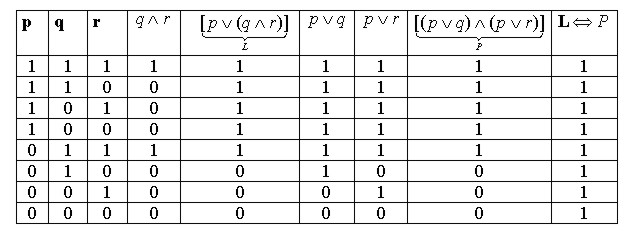
Ponieważ w ostatniej kolumnie występują tylko ,,jedynki”, więc dane zdanie jest zawsze prawdziwe, czyli jest tautologią.

 

Zwroty ,,dla każdego...” lub ,,istnieje...” zapisujemy wykorzystując kwantyfikatory. Wyrażenie ,,dla każdego x...” nazywamy kwantyfikatorem ogólnym i zapisujemy symbolicznie :, gdzie p(x) jest dowolną formułą zdaniową. Z kolei wyrażenie ,,istnieje takie xnazywamy kwantyfikatorem szczegółowym i zapisujemy symbolicznie: .

      

 

TWIERDZENIE

                                ~

                                ~

 

Przykłady:

Zapisz poniższe zdania ,stosując kwantyfikatory a następnie zapisz zaprzeczenia tych zdań- słownie i symbolicznie.

a)      p: Każde dwie liczby naturalne są równe

b)      q: Istnieje liczba wymierna większa od 3

c)      r: Każda liczba naturalna jest nieujemna

d)      s: Istnieje liczba naturalna m taka, że jeśli m >5, to m²

 

Rozwiązania:

a) p:                 ~ p: Istnieją liczby naturalne, które są różne             ~ p:

b) q:                      ~ q: Każda liczba wymierna jest niewiększa niż 3          ~ q:

c) r:                       ~ r: Istnieje liczba naturalna mniejsza od zera                 ~ r:

d) s:     ~ s: Każda liczba naturalna m jest taka, że m>5 i m² = 6

    ~ s:

Darmowy hosting zapewnia PRV.PL