1. Wzajemne położenie dwóch prostych:
Proste na płaszczyźnie mogą być równoległe lub przecinające się, natomiast proste w przestrzeni mogą być równoległe, przecinające się lub skośne.

| Proste k i l przecinają się. |
| Proste l i m są do siebie równoległe. |
| Proste k i m są skośne: nie są równoległe i nie przecinają się. Proste skośne nie występują na jednej płaszczyźnie. |
Wzajemne położenie prostej i płaszczyzny:
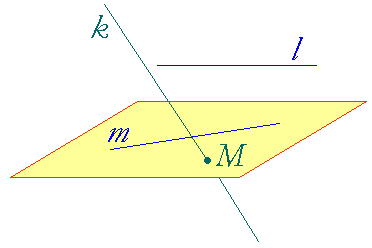
Prostą nazywamy równoległą do płaszczyzny, gdy nie ma ona punktów wspólnych z płaszczyzną (prosta l) lub zawiera się w tej płaszczyźnie (prosta m).
Jeżeli płaszczyzna i prosta mają dokładnie jeden punkt wspólny to mówimy, że prosta (prosta k) przecina (przebija) płaszczyznę.
-
Jeżeli prosta jest równoległa do prostej zawartej w płaszczyźnie, to jest do tej płaszczyzny równoległa.
-
Przez każdy punkt przestrzeni przechodzi nieskończenie wiele prostych równoległych do danej płaszczyzny.
Wzajemne położenie dwóch płaszczyzn w przestrzeni:
Dwie płaszczyzny mogą być do siebie równoległe (nie mają punktów wspólnych) lub mogą się przecinać (częścią wspólną jest prosta).
2. Jeżeli prosta nie jest prostopadła do płaszczyzny, to kątem nachylenia prostej do płaszczyzny nazywamy kąt utworzony przez tę prostą i jej rzut prostokątny na daną płaszczyznę.
Kąt między płaszczyznami jest to kąt między wektorami prostopadłymi do tych płaszczyzn.
3. Wielościan jest to bryła ograniczona wielokątami ułożonymi w taki sposób, że każdy bok wielokąta jest wspólnym bokiem dwóch wielokątów. Wielokąty te nazywamy ścianami wielościanu, boki wielokątów - krawędziami, a wierzchołki - wierzchołkami wielościanu.
Ostrosłupem nazywamy wielościan, którego jedna ściana (zwana podstawą) jest dowolnym wielokątem, a pozostałe ściany (nazywane ścianami bocznymi) są trójkątami o wspólnym wierzchołku S, który nazywamy wierzchołkiem ostrosłupa.
Ostrosłupem prawidłowym nazywamy ostrosłup, którego podstawą jest wielokąt foremny i którego spodek wysokości pokrywa się ze środkiem okręgu opisanego na jego podstawie.
Czworościanem nazywamy ostrosłup, którego wszystkie ściany są trójkątami.
Graniastosłupem nazywamy wielościan, którego dwie ściany (zwane podstawami), są przystającymi wielokątami leżącymi w płaszczyznach równoległych, a pozostałe ściany (zwane ścianami bocznymi) są równoległobokami, których wszystkie wierzchołki są jednocześnie wierzchołkami podstaw.
Graniastosłup prosty, to graniastosłup, w którym krawędzie boczne są prostopadłe do podstaw.
Graniastosłup prawidłowy to graniastosłup prosty, którego podstawy są wielokątami foremnymi.
Równoległościan to graniastosłup, którego wszystkie ściany są równoległobokami.
Prostopadłościan to graniastosłup, którego wszystkie ściany są prostokątami.
4. Wielościanem foremnym nazywamy wielościan wypukły , którego wszystkie ściany są przystającymi wielokątami foremnymi i każdy jego wierzchołek jest końcem tej samej liczby krawędzi wielościanu.
Istnieje pięć wielościanów foremnych: czworościan foremny, sześcian, ośmiościan foremny, dwunastościan foremny, dwudziestościan foremny.
Twierdzenie Eulera:
W wielościanie wypukłym liczba wierzchołków w, liczba ścian s i liczba krawędzi k spełniają równość:
w - k + s = 2
5. Wzory na objętości wielościanów i ich pola powierzchni.
Objętością graniastosłupa nazywamy iloczyn pola podstawy przez wysokość poprowadzoną do tej podstawy.
Objętością ostrosłupa nazywamy trzecią część iloczynu pola podstawy przez wysokość.
Polem powierzchni bryły nazywamy sumę pól wszystkich ścian wielościanu.
Jeżeli figura f i prosta k zawarte są w jednej płaszczyźnie, to figurą otrzymaną przez pełny obrót figury f wokół prostej k nazywamy figurą obrotową. Prostą k nazywamy osią obrotu tej figury.
Walcem nazywamy bryłę obrotową powstałą przez obrót prostokąta dookoła prostej zawierającej jeden z boków prostokąta. Bok prostokąta zawarty w osi obrotu jest wysokością walca, a drugi jego bok jest promieniem podstawy walca.
| H - wysokość walca |
| r - promień podstawy walca |
| Pp - pole powierzchni całkowitej walca |
| V - objętość |
V = p r2·H
Pp = 2·p r2+2p r·H = 2p r·(r + H)
Stożkiem nazywamy bryłę obrotową powstałą przez obrót trójkąta prostokątnego dookoła prostej zawierającej jedną z przyprostokątnych.
| H - wysokość stożka |
| r - promień podstawy stożka |
| l - tworząca stożka |
| Pc - pole powierzchni całkowitej stożka |
| Pp - pole podstawy |
| Pb - pole powierzchni bocznej stożka |
| V - objętość |
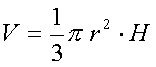
Pc = Pb + Pp = p rl + p r2 = 2p r·(r + H)
Kulą o środku O i promieniu R nazywamy zbiór wszystkich punktów w przestrzeni, których odległość od punktu O jest nie większa od R. Kula jest figurą obrotową powstałą przez obrót półkola dookoła prostej, w której zawarta jest średnica tego półkola.
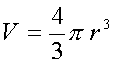
Pp = 4p r2
7. Krzywe stożkowe to krzywe, które powstają z przecięcia powierzchni stożkowej obrotowej płaszczyzną nie przechodzącą przez jej wierzchołek.
| a - kąt jaki tworzy płaszczyzna krzywej z wysokością stożka |
| b - kąt jaki tworzy wysokość z tworzącą stożka |
| Jeśli a > b, krzywą stożkową jest elipsa. |
| Jeśli a = b, krzywą stożkową jest parabola. |
| Jeśli a < b, krzywą stożkową jest hiperbola. |