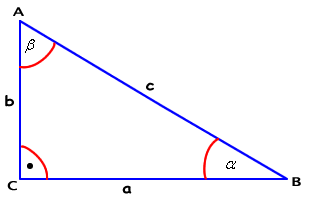
 |
|
|
c - przeciwprostokątna | |
|
a - przyprostokątna przeciwległa kątowi
| |
|
b - przyprostokątna przeciwległa kątowi
|
|
|
|
|
c - przeciwprostokątna | |
|
a - przyprostokątna przeciwległa kątowi
| |
|
b - przyprostokątna przeciwległa kątowi
|
|
Sinusem kąta ostrego alfa w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przeciwległej temu kątowi do długości przeciwprostokątnej. |
 |
|
Cosinusem kąta ostrego alfa w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przyległej do tego kąta do długości przeciwprostokątnej. |
|
|
Tangensem kata ostrego alfa w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przeciwległej temu kątowi do długości drugiej przyprostokątnej. |
 |
|
Cotangensem kąta ostrego alfa w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przyległej do tego kąta do długości drugiej przyprostokątnej. |
 |
|
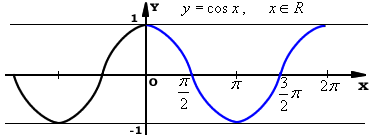
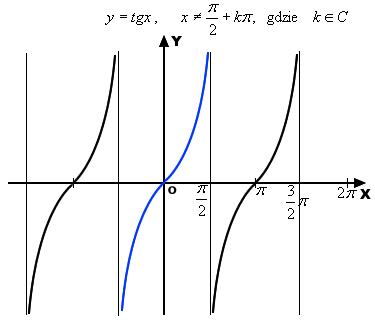
Wykresy funkcji trygonometrycznych |
|
 |
 |
 |
 |
|
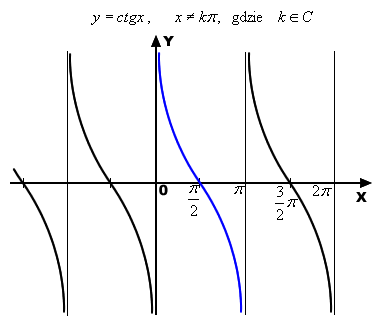Tabela znaków funkcji trygonometrycznych w poszczególnych ćwiartkach | ||||
|
I |
II |
III |
IV | |
 |
+ |
+ |
- |
- |
 |
+ |
- |
- |
+ |
 |
+ |
- |
+ |
- |
 |
+ |
- |
+ |
- |
Związki między funkcjami trygonometrycznymi tego samego kata |
|
 |
 |
|
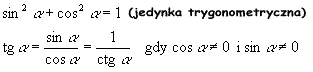Funkcje |  |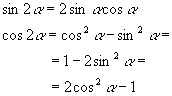
 |
|
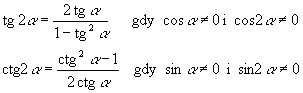Funkcje |
|
|
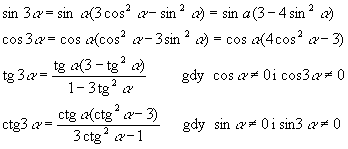
Funkcje |
 |
|
"+" lub "-" wybieramy zależnie od tego, do której "ćwiartki" należy końcowe ramię kąta |
|
 |
|
Funkcje |
 |
|
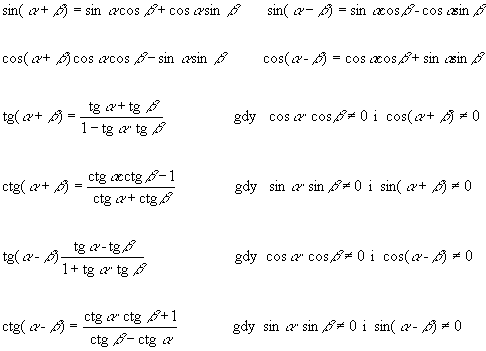Suma |
|
|
Tabela wartości funkcji trygonometrycznych dla niektórych miar kąta |
||||||||||||||
|
x |
0 |
|
|
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
 |
|
0o |
15o |
22.5o |
30o |
45o |
60o |
90o |
120o |
135o |
150o |
180o |
225o |
270o |
360o |
|
|
sin x |
0 |
 |
 |
|
 |
 |
1 |
|
|
|
0 |
 |
-1 |
0 |
|
cos x |
1 |
 |
 |
|
|
|
0 |
 |
 |
 |
-1 |
|
0 |
1 |
|
tg x |
0 |
 |
 |
 |
1 |
 |
nie |
 |
-1 |
 |
0 |
1 |
nie |
0 |
|
ctg x |
nie |
 |
 |
|
1 |
|
0 |
|
-1 |
|
nie |
1 |
0 |
nie |
|
Jednostki
miary |
Miara stopniowa |
Miara łukowa |
Miara gradusowa |
|
1o
- jeden stopień |
1 rad - jeden radian radianem nazywamy miarę kąta środkowego opartego na łuku o długości równej promieniowi okręgu.  |
1g - jeden gradus 1/100 - kąta prostego, |
- kąty ostre w trójkącie prostokątnym