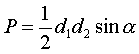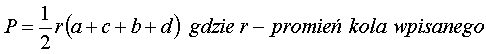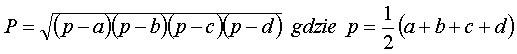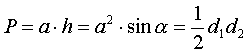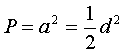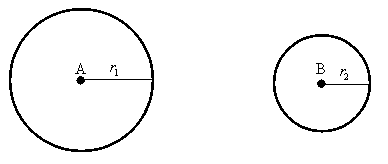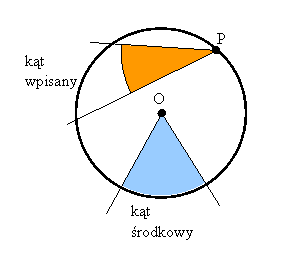|
1. Wielokąt foremny i wypukły
|
top |
Wielokątem foremnym nazywamy wielokąt, w którym
każde dwa boki są równe i każde dwa kąty są równe. Na każdym wielokącie
foremnym można opisać okrąg (o promieniu R)
i w każdy wielokąt foremny można wpisać okrąg (o
promieniu r - apotema wielokąta foremnego). Okręgi te są
współśrodkowe to znaczy, że mają wspólny środek, który nazywamy środkiem
wielokąta.
W wielokątach foremnych o n-bokach
:
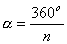
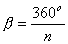
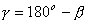
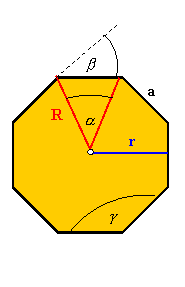
Bok wielokąta foremnego.
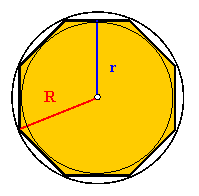
Pole wielokąta foremnego:
- z zastosowaniem miary
stopniowej kąta
- z zastosowaniem miary
łukowej kąta
Zależności w niektórych wielokątach foremnych:
Wielokąt wypukły
Jeśli liczba boków jest równa n, to suma kątów
wewnętrznych jest równa:
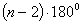
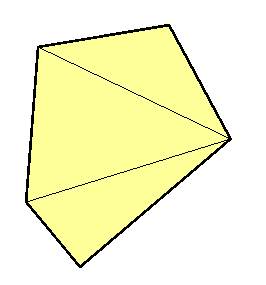
Pole wielokąta wypukłego
Pole oblicza się dzieląc wielokąt wypukły na trójkąty.
Wielokąt wypukły jest foremny, jeżeli ma wszystkie boki
równe i kąty równe.
W każdym
n-kącie liczba przekątnych wynosi:
a
suma miar kątów zewnętrznych wynosi 360°.
Czworokątem (czworobokiem) nazywamy wielokąt o
czterech bokach. Suma kątów każdego czworokąta jest równa 360°.
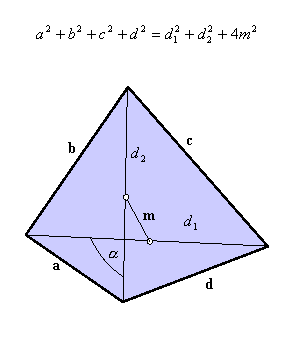
m - odcinek
łączący środek przekątnej
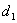ze
środkiem przekątnej
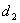
Pole czworokąta
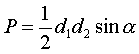
gdzie
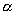jest
kątem między przekątnymi.
Obwód czworokąta
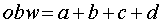
Czworokąt wypukły można opisać na okręgu wtedy i tylko
wtedy, gdy:
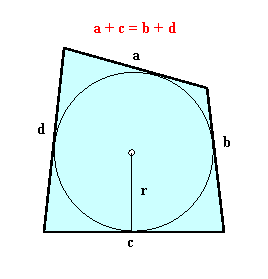
Pole czworokąta opisanego na okręgu
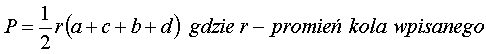
Czworokąt wypukły można wpisać w okrąg wtedy i tylko
wtedy, gdy:
Pole czworokąta wpisanego w okrąg
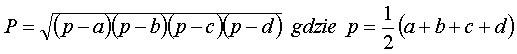
Twierdzenie
Ptolemeusza
Trapezem nazywamy czworokąt, który ma przynajmniej
jedną parę boków równoległych. Boki równoległe ( a i b) nazywamy
podstawami trapezu.
Oznaczenia:
- a,b
- podstawy trapezu
- h - wysokość
trapezu
- m - linia środkowa
(prosta równoległa do podstaw, łącząca środki nierównoległych boków trapezu)
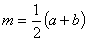
Pole trapezu
Trapez jest równoramiennym wtedy, gdy jego boki
nierównoległe (c i d) są równe.
Pole trapezu równoramiennego
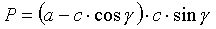
Rombem nazywamy
równoległobok, którego wszystkie boki są równe, przekątne są wzajemnie
prostopadłe i dzielą kąty na połowy.
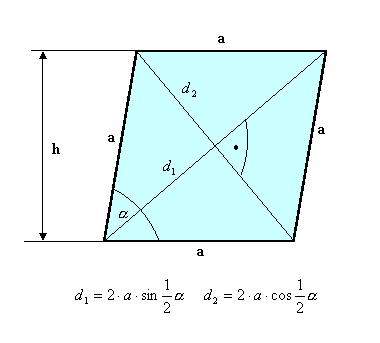
Pole rombu
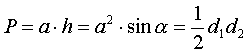
Równoległobokiem
nazywamy
czworokąt, w którym przeciwległe boki są parami równe i równoległe. Punkt
Q (punkt przecięcia się przekątnych) dzieli przekątne na połowy. Przeciwległe
kąty są parami równe.
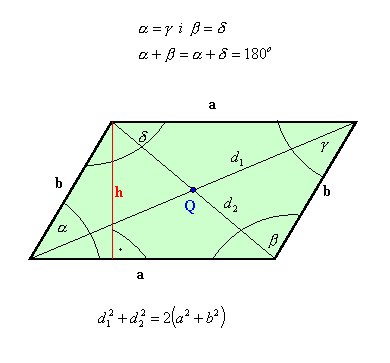
Pole równoległoboku
Kwadratem nazywamy
równoległobok, w którym wszystkie boki są równe, wszystkie kąty są proste i
przekątne są równe.
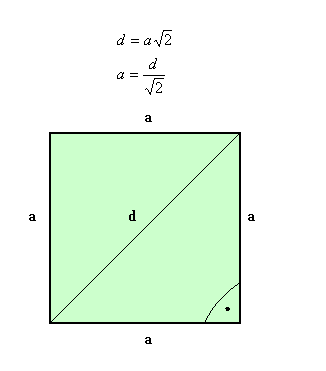
Pole kwadratu
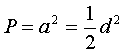
Prostokątem nazywamy
równoległobok, w którym wszystkie kąty są proste i przekątne są równe.
Pole prostokąta
Deltoid.
Czworokąt jest deltoidem:
- jeżeli a = b i c
= d
- przekątne są wzajemnie
prostopadłe (przekątna
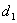dzieli
przekątną
na
połowy i odwrotnie)
- kąt miedzy bokami a
i d jest równy kątowi między bokami b i c
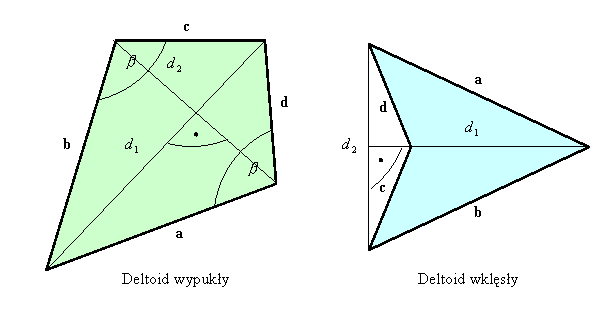
Pole deltoidu
|
9. Okrąg dziewięciu punktów |
top |
Definicja okrągu dziewięciu punktów
W dowolnym
trójkącie ABC środki boków K,
L
i M,
spodki wysokości D,
E i
F oraz środki odcinków
łączących
ortocentrum tego trójkąta H
(punkt przecięcia wysokości) z jego wierzchołkami - punkty
X,
Y i
Z leżą na jednym okręgu
Okrąg ten nazywamy jako okrąg
dziewięciu punktów lub okrąg Feuerbacha.
Aby narysować okrąg
dziewięciu punktów należy:
- zaznaczyć dowolne 3 punkty (A,B,C), które
łączymy ze sobą rysując trójkąt ABC
- na każdym boku zaznaczamy
punkty środkowe K, L, M.
- z wierzchołka C wyznaczamy
wysokość na bok AB. Punkt rzutu prostokątnego z wierzchołka C
na prostą zawierającą przeciwległy bok oznaczamy literą
D.
-
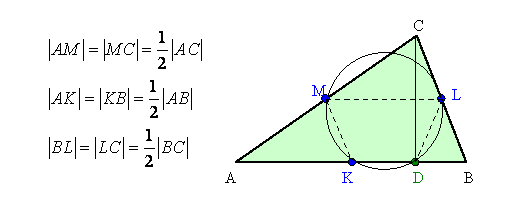
czworokąt KDLM jest
trapezem równoramiennym, a jak wiemy na każdym trapezie równoramiennym
da się opisać okrąg, więc punkty K,
D, L,
M, leżą na tym samym okręgu.
- z wierzchołka A wyznaczamy
wysokość na bok BC (punkt rzutu prostokątnego z wierzchołka A
na prostą zawierającą przeciwległy bok oznaczamy literą
E) i z wierzchołka B wyznaczamy
wysokość na bok AC (punkt rzutu prostokątnego z wierzchołka B
na prostą zawierającą przeciwległy bok oznaczamy literą
F), ich rzuty będą również leżały na
tym samym okręgu.
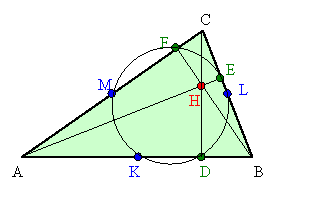
- zaznaczamy środek odcinka łączącego
ortocentrum H z
wierzchołkiem A i oznaczamy jako X,
środek odcinka łączącego
ortocentrum H z
wierzchołkiem B i oznaczamy jako Y,
środek odcinka łączącego
ortocentrum H z
wierzchołkiem C i oznaczamy jako Z.
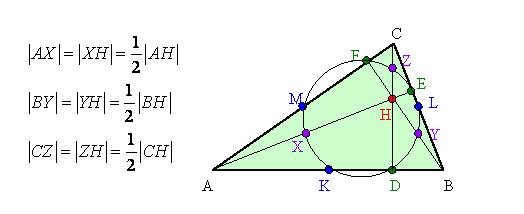
W ten sposób otrzymujemy okrąg 9 - ciu punktów.
Objaśnienia:
Spodkiem wysokości
nazywamy, punkt wspólny wysokości i prostej zawierającej odpowiedni bok
trójkąta.
|
10. Trójkąt prostokątny |
top |
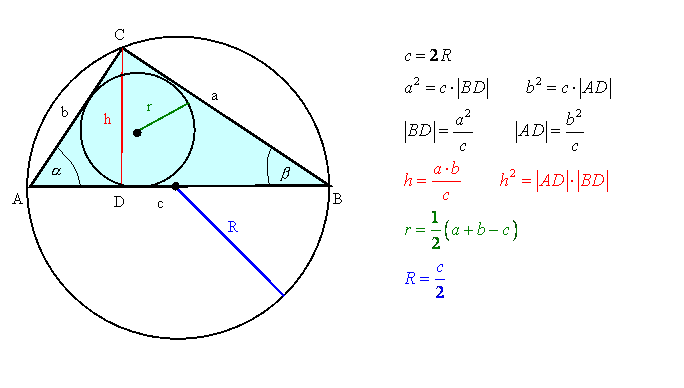
Pole trójkąta
Wzory trygonometryczne dotyczące trójkąta
prostokątnego
Twierdzenie Pitagorasa
Jeżeli trójkąt jest prostokątny, to suma kwadratów
długości przyprostokątnych jest równa kwadratowi przeciwprostokątnej.
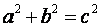
Twierdzenie odwrotne do twierdzenia Pitagorasa
Jeżeli w trójkącie kwadrat długości jednego boku równa
się sumie kwadratów długości boków pozostałych, to trójkąt jest prostokątny.
Okręgiem
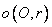o
środku O i promieniu r>0 nazywamy zbiór wszystkich punktów
płaszczyzny, których odległość od punktu O jest równa r.
Kołem
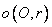o
środku O i promieniu r>0 nazywamy zbiór wszystkich punktów
płaszczyzny, których odległość od punktu O nie jest większa od r.
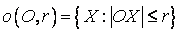
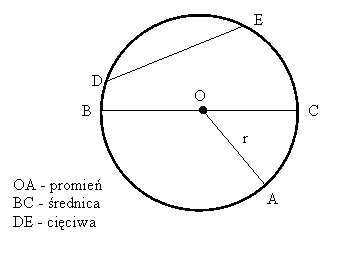
Średnica okręgu przechodząca przez
jego środek jest równa 2r, gdzie r - promień koła.
Średnica koła jest większa od każdej cięciwy niebędącej
średnicą.
Średnica prostopadła do cięciwy dzieli tę cięciwę na
połowy.
Cięciwa okręgu,
to prosta łącząca dwa punkty (D i E) leżące na powierzchni
okręgu, niemająca żadnych innych wspólnych punktów z powierzchnią.
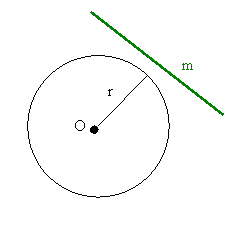
Jeżeli dany jest okrąg
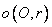i
prosta m to:
- m
jest styczną
do okręgu wtedy i tylko wtedy, gdy odległość O od
m równa jest r
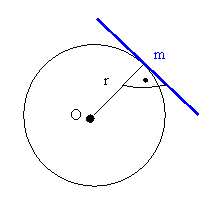
Styczna do okręgu jest prostopadła do promienia okręgu
poprowadzonego do punktu styczności.
- m
jest sieczną okręgu wtedy i
tylko wtedy, gdy odległość O od m
jest mniejsza od r.
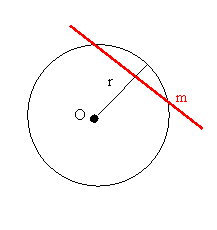
- m
jest zewnętrzną dla
okręgu wtedy i tylko wtedy, gdy odległość O od
m jest większa od r.
Jeżeli dane są dwa różne okręgi
to:
- okręgi są wzajemnie zewnętrzne wtedy i tylko
wtedy, gdy
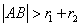
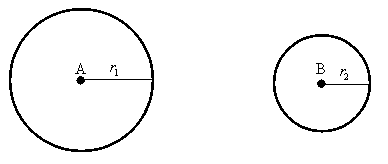
- okręgi są styczne
zewnętrznie wtedy i tylko wtedy, gdy
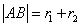
- okręgi są przecinające
się wtedy i tylko wtedy, gdy
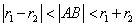
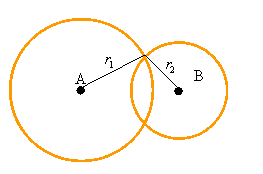
Objaśnienie: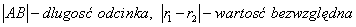
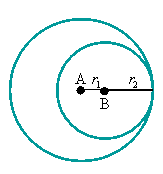
- okręgi są styczne
wewnętrznie wtedy i tylko wtedy, gdy
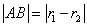
Objaśnienie: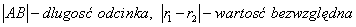
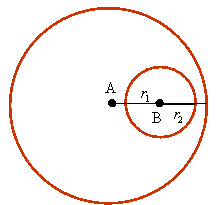
Kąt środkowy
Kąt, którego wierzchołek jest środkiem okręgu
nazywamy kątem środkowym
Kąt wpisany.
Kątem wpisanym w okrąg nazywamy kąt
wypukły, którego wierzchołkiem jest dowolny punkt P okręgu a ramionami
półproste zawierające
cięciwy okręgu przecinające się w punkcie P.
W okręgu równym kątom środkowym odpowiadają równe
cięciwy.
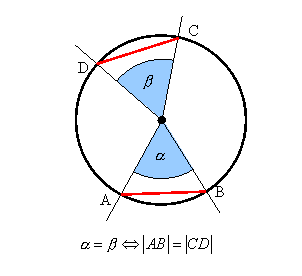
Kąty wpisane w okrąg i oparte na tym samym łuku są równe
i każdy z nich jest równy połowie kąta środkowego opartego na tym samym łuku,
co kąty wpisane.
Kąt ostry między cięciwą i styczną przechodzącą przez
koniec tej cięciwy jest równy połowie kąta środkowego odpowiadającego tej
cięciwie.
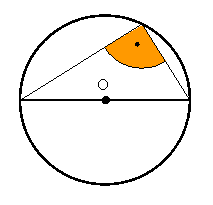
Kąt wpisany oparty o
średnicę jest prosty.
|
Wektorem nazywamy uporządkowaną parę punktów. Pierwszy
z tych punktów nazywamy początkiem wektora albo punktem zaczepienia
wektora, a drugi - końcem wektora.
Wektor o początku A i końcu B oznaczamy
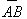i przedstawiamy na rysunku w postaci odcinka AB zakończonego w punkcie B
grotem. |
|
Jeżeli wektor
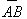jest zawarty w osi liczbowej, to długość wektora
,
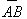przy obranej i ustalonej jednosce długości:
|
|
a) ze znakiem plus, jeżeli wektor
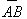ma zwrot zgodny ze zwrotem osi
|
| b) ze znakiem minus, jeżeli wektor
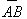ma zwrot przeciwny do zwrotu osi |
| nazywamy miarą względną wektora
.
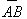Miarę wektora
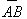, zawartego w
osi liczbowej zapisujemy, używając symbolu AB. |
Każdy wektor ma miarę bezwzględną (długość), która jest
zawsze liczbą dodatnią, natomiast wektor zawarty w osi liczbowej, oprócz
miary bezwzglednej ma jeszcze miarę względną.
Wektorem zerowym nazywamy wektor, którego początek i koniec pokrywają
się. Wektor zerowy oznaczamy zerem: 0. |
 |
|
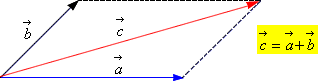
| zasada równoległoboku |
 |
| zasada trójkąta |
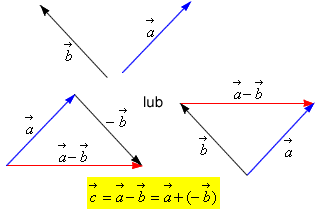
Różnicą wektorów
i 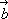 jest wektor równy sumie wektora
i wektora przeciwnego do wektora
. |
|
 |
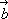Darmowy hosting zapewnia PRV.PL
